对抗攻击之FGSM

2018-11-02

　　对抗样本的攻防是一个非常有趣的领域，它引发了我们的思考：当前模型的准确率是否只是徒有其表，并没有真正学习到内在的语义信息，无法应对泛化问题

　　本文仅从对抗攻击出发，介绍一种简单的对抗样本生成算法fast gradient sign method（FGSM）

什么是对抗攻击

　　算法之前，先介绍一下对抗攻击的基本概念

　　对抗攻击最核心的手段就是制造对抗样本去迷惑模型，比如在计算机视觉领域，攻击样本就是向原始样本中添加一些人眼无法察觉的噪声，这些噪声不会影响人类识别，但却很容易迷惑机器学习模型，使它作出错误的判断

对抗攻击的分类

无目标的对抗攻击：只是让目标模型的判断出错

有目标的对抗攻击：引导目标模型做出我们想要错误判断（比如我们想要让分类器将猫识别为狗）

以对目标模型的了解程度为标准，对抗攻击又可以分成白盒攻击和黑盒攻击

白盒攻击：在已经获取机器学习模型内部的所有信息和参数上进行攻击

黑盒攻击：在神经网络结构为黑箱时，仅通过模型的输入和输出，逆推生成对抗样本。

FGSM基本原理

　　Fast Gradient Step Method（FGSM）是一种简单但是有效的对抗样本生成算法

　　x*表示对抗样本，x表示原样本，J（）表示代价函数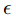，是手动设置的超参

　　直观来看就是在输入的基础上沿损失函数的梯度方向加入了一定的噪声，使目标模型产生了误判

　　这个线性组合的式子乍一看非常简单，可要明白它为什么有效还是得从对抗样本的线性解释说起

对抗样本的线性解释：

　　对输入x加入一个小小的扰动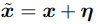，如果这个扰动小于模型的精度，那么它会被模型忽略，但是这个扰动会随着输入被模型参数放大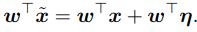为了最大化扰动的影响，我们可以取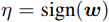，sign函数可以保证扰动与梯度方向一致，这样就可以对分类结果有最大的影响，而且当输入的维度越大，攻击的累积效果越明显

　　我的理解是

沿梯度方向可以使样本更容易越过既定的分类边界，从而形成误判

　　回到上面的式子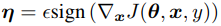，J( , ,)代表损失函数，对于某个特定的模型而言，FGSM将损失函数近似线性化（对于神经网络而言，很多神经网络为了节省计算上的代价，都被设计成了非常线性的形式，这使得他们更容易优化，但是这样”廉价”的网络也导致了对于对抗扰动的脆弱性）

也就是说，即是是神经网络这样的模型，也能通过线性干扰来对它进行攻击

实例

　　究竟FGSM的效果如何，不如动手试一试

　　环境：python3.5 + tensorflow

　　数据集：MNIST

　　目标：用FGSM实现non-targeted attack

　　为了实现对抗攻击，我们首先要训练一个被攻击的模型，这里用tensorflow实现了一个MNIST分类模型，网络结构如下

# Convolution layer 1 - 32 x 5 x 5 
# Conv -> BatchNorm -> Relu -> Max_pool
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
x_conv1 = conv2d(x_image, W_conv1) + b_conv1
y1 = tf.nn.relu(tf.layers.batch_normalization(x_conv1))
x_pool1 = max_pooling_2x2(y1)

# Conv layer 2 - 64 x 5 x 5
# Conv -> BatchNorm -> Relu -> Max_pool
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
x_conv2 = conv2d(x_pool1, W_conv2) + b_conv2
y2 = tf.nn.relu(tf.layers.batch_normalization(x_conv2))
x_pool2 = max_pooling_2x2(y2)

# Flatten 
x_flat = tf.reshape(x_pool2, [-1, 7 * 7 * 64])

# Dense fully connected layer
W_fc1 = weight_variable([7 * 7 * 64, 1024]) # max pooling reduced image to 7x7
b_fc1 = bias_variable([1024])
x_fc1 = tf.nn.relu(tf.layers.batch_normalization(tf.matmul(x_flat, W_fc1) + b_fc1))

# Dropout
keep_prob = tf.placeholder(tf.float32)
x_fc1_drop = tf.nn.dropout(x_fc1, keep_prob)

# Classification layer
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv = tf.matmul(x_fc1_drop, W_fc2) + b_fc2

　　在训练了1000epoches后，在训练集和测试集上分别达到了0.98和0.965的准确度

　　接下来用FGSM生成对抗样本（本人硬件设备更不上，只能分batch做）

test_accuracy = 0
for i in range(100):
    batch = mnist.test.next_batch(100)
    batch = list(batch)
    # FGSM
    gradient = img_gradient.eval({x: batch[0], y_: batch[1], keep_prob: 1.0})
    batch[0] = batch[0] + 0.02 * np.sign(gradient)
    test_accuracy += accuracy.eval(feed_dict={x:batch[0], y_: batch[1], keep_prob: 1.0})
    print("Batch %d: test accuracy %g" % (i + 1, test_accuracy / (i + 1)))
print("total test accuracy %g"%(test_accuracy / 100))

　　最终在测试集上的准确率降到了0.8925，说明FGSM还是起到了一定的作用的

　　为了对FGSM有一个更直观的了解，我随机抽取了10个实际值为“2”的数据，下面依次为10个数据的预测值，可以看到模型在这10个数据上的准确率是100%

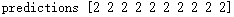
　　这是其中的一例：

　　下面基于这10个随机样本，使用FGSM进行对抗样本的生成（单次FGSM的效果一般，为了使实验结果更加明显，这里采用了Iterative-FGSM，也就是多次迭代的FGSM，steps代表迭代次数）

adversarial_img = original_images.copy()
adv_img_hist = list() # store adv_img
for i in range(0, steps):
    gradient = img_gradient.eval({x: adversarial_img, y_: original_labels, keep_prob: 1.0})
    # Update using sign of gradient
    adversarial_img = adversarial_img + step_size * np.sign(gradient)
    adv_img_hist.append(adversarial_img)
    prediction = tf.argmax(y,1)
    prediction_val = prediction.eval(feed_dict={x: adversarial_img, keep_prob: 1.0}, session=sess)
    print("predictions", prediction_val)

　　这里进行了10次迭代，可以看到，模型发生了很明显的误判

　　对比一下原始样本和对抗样本，肉眼几乎察觉不到什么差别，但模型给出的结果却截然不同

　　（左、中、右依次为：原始样本、噪声、对抗样本）

　　（模型对原始样本给出的判断是“2”，对对抗样本给出的判断是“3”）

未来的研究方向

如何利用对抗训练有效地训练出能抵抗对抗攻击的模型？
分类边界到底是什么样的？
如何判断对抗样本的存在？

参考

《Explaining and Harnessing Adversarial Examples》

https://blog.ycombinator.com/how-adversarial-attacks-work/

https://cloud.tencent.com/developer/article/1167792